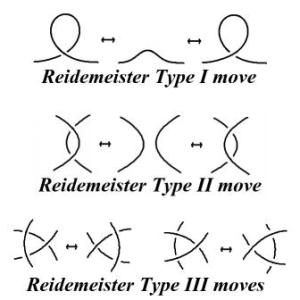
(The above figure shows the three fundamental moves that one can use in Knot theory to see whether two knots are equivalent.)
Background : Well, Knot theory is an interesting part of mathematical physics with a lot of applications in diverse fields. It does not fit directly into the standard curriculum for the five basic themes of undergrad-theoretical-physics ( Classical, Quantum, Statistical, Field theoretic and Mathematical methods) .
So, this is just for fun – and like many other things in life done for fun , you should be open-minded enough to learn new things as you go along. I can’t guarantee that you would understand everything here ( partly because I don’t understand everything and mainly because nobody understands everything 😉 ), but it is fun if you like it.
Note that Knot theory to start with does not require much background in physics ( It is afterall a branch of topology and so much of the required background is from the math side ). But, if you really want to see some beautiful ways Knot theory enters physics, you should have a background in Quantum field theory( in particular some familiarity with Feynman’s diagrammatic way of doing perturbation theory and path integrals at the level of say Quantum Field Theory in a Nutshell by A. Zee) .
As always, if you have no idea what Knot theory is about, you can do no better than start off with the article on Knot theory from Wikipedia and then proceed to different sites which talk about knot theory Then there is a site which has enough links to keep you busy throughout the summers 🙂 This should give you an idea of what is this all about.
If you are not in mood for all this stuff, then you might like to read some stories ! Here is an interesting article titled Scottish Physics and Knot Theory’s Odd Origins which talks about the history of knot theory and how Kelvin invented it for modelling vortices in ether 🙂 It talks about the role played by Maxwell, Kelvin and Tait(He is a mathematician who is supposed to have invented dimples in the golf ball ;)) in Knot theory. A bit more serious article is A brief history of knot theory which I got from here.
Now, for some serious stuff. This is A Knot Theory Primer. See also Knot Knotes by J.D.Roberts which I found at this site having lots of good books on physics and math( I am thinking of a separate post for that site, so that people don’t miss it ). You can also see a short course by Kauffman.
Ok, I’ve come so far and I’ve not even come to the QFT applications of Knot theory many of which go under the name of Witten. Since, this post has already become so long, I will just point you to an AJP article before I finish.
Knots and physics: Old wine in new bottles
(Should be accessible inside IITK)
Allen C. Hirshfeld
Physics Department, The University of Dortmund, D-44221 Dortmund, Germany
(Received 3 July 1997; accepted 15 May 1998)
The history of the interplay between physics and mathematics in the theory of knots is briefly reviewed. In particular, Gauss’ original definition of the linking number in the context of electromagnetism is presented, along with analytical, algebraical, and geometrical derivations. In a modern context, the linking number appears in the first-order term in the perturbation expansion of a Wilson loop in Chern–Simons quantum field theory. New knot invariants, the Vassiliev numbers, arise in higher-order terms of the expansion, and can be written in a form which shows them to be generalizations of the linking number. ©1998 American Association of Physics Teachers.
Update(10/5) : Ok, I give in to temptation. I can’t just leave a post on Knot theory without talking more about its relations with Topological Quantum Field theories. One of the landmark papers in this field is of course Witten’s Quantum field theory and the Jones polynomial. But, since it is a bit high-brow stuff, it is better to start with an article on that paper. ( you can also see a talk by Witten where he talks about the period when this paper was written.) By the way, If I remember correctly, it is this paper which led to Witten’s Field’s medal…
Try your hands at “Quantum Topology and Quantum Computing”, by Kauffman and “Quantum Topology and the Jones Polynomial”, by Kauffman . Lots of pages in the first paper are devoted to introducing quantum mechanics so you can just skip it if you feel like it.
Leave a Response »






